INTRODUCTION
Mathematical models play a crucial role in the interpretation of drug release mechanism (Gouda et al., 2017; Grassi et al., 2006; Paarakh et al., 2018; Varma et al., 2004). The drug release kinetics for given formulations has been usually fitted to predefined semi-empirical models using non-hierarchical frequentist modelling approach. The appropriate model for each formulation is selected based on the highest Rsq (Adjust) and the lowest Akaike Information Criterion (AIC) (Gouda et al., 2017; Paarakh et al., 2018; Victor and Francis, 2017). Such a situation may lead to variation in the best-fitting model among formulations, in particular when the number of points in the curve is limited. This is not meaningful biologically given the interdependency between data and the model convergence may be problematic (Piray et al., 2019). Hierarchical Bayesian modelling can solve these issues by expressing the model over all formulations and consequently addressing both model fitting and model comparison within the same framework (Piray et al., 2019). Hierarchical Bayesian modelling approach assumes that the formulations share the same best model and differ only in some or all parameters values of the model (Andrews et al., 2002; Millar, 2009; Wiecki et al., 2013). The differences between the two statistical concepts have their root in differing conceptions of probability. In practice, frequentist approach quantify the properties of data-derived quantifies, as for Bayesian approach quantify the incertitude of measure (VanderPlas, 2014).
For pharmaceutical development, the application of Bayesian statistics remains modest and mainly affects the field of clinical trials and not the field of formulation. This will be one of the strongest points of our formulation study (Natanegara et al., 2014; Price and LaVange, 2014) .
The use of polymers in the drug delivery system increased during the last years as a result of the advantages offered by these molecules (Andrews et al., 2002; Malekmohammadi et al., 2019;; Zuo et al., 2014).For sustained-release system, Eudragits, good safety profile molecules, may give the formulator the possibility of choosing between different categories depending on the purpose of the formulation such as oral, colon, rectal, and even transdermal (Joshi, 2013; Nikam et al., 2011; Thakral et al., 2013). For clonic targeting, both Eudragit L-100 and S100 are widely used for molecule delivery as they offer muco-adhesiveness and pH-dependent release (Khan et al., 1999; Lee et al., 2020). Only one study has been reported in the scientific literature on the use of these polymers in rectal drug delivery (Baloglu et al., 2002). In this study, authors prepared and evaluated the kinetics of sustained-release suppositories of polyethylene glycol (PEG) 400, PEG 4000, Witepsol, and Eudragit L-100. In our study, the choice of these Eudragits comes from the fact that the physiological conditions of the colon (especially the distal colon) and those of the rectum were similar for the pH (pH = 7–8); hence, the interest of these polymers called pH-Dependent Drug Delivery Systems in the formulation of Hydrophilic suppositories (Hua, 2019; Lee et al., 2020). By optimizing the mixture composition of these polymers (EL-100 and ES-100) and the total polymers content of the matrix, a specific release rate for the active molecule can be obtained by modifying the diffusivity through the gelled of the matrix structure (Di Colo et al., 2002; Misra, 2014; Nikam et al., 2011; Surti et al., 2020).
The novelty of this study is the combination of two Eudragit polymers in the formulation of sustained release suppositories and the application of the Bayesian hierarchical approach to the modeling of the release kinetics. The first objective of this study is to use the hierarchical Bayesian modeling approach to select the appropriate empirical kinetics model of Barbital sustained release. The second objective is to optimize the in vitro release rate of sustained-release suppository by controlling the composition of E-L100 and E-S100 in the experimental mixture.
MATERIALS AND METHODS
Materials
All the materials used in this study, i.e., “Sodium Barbital”, PEG 6000, Eudragit® L100, Eudragit® S100 (Rohm Pharma, GmbH, Germany), NaH2PO4 (monobasic), and Na2HPO4 (dibasic) were acquired by the galenic pharmacy laboratory of the Faculty of Medicine and Pharmacy.
Design of experiments and statistical analysis
In the present study, we used a personalized design of experiment with constraint and with process factor, which was time. The quantities of the two Eudragits varied from 0 to 2 g each, with upper constraint of 2 g for the sum of the two Eudragits L and S, based on preliminary tests. Beyond this limit, there would be little flow, poor filling of the metal molds, and an unacceptable appearance of the prepared suppositories. The quantity of Macrogol 6000 and Barbital were set to 17.4 and 0.6 g, respectively (Table 1). For each of the 13 formulations, three experiments was made and five sampling performed at 20, 50, 80, 160, and 235 minutes.
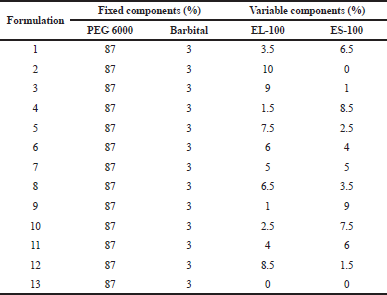 | Table 1. Matrix of experiments with proportions of fixed (PEG 6000 and Barbital) and variable (EL-100 and ES-100) components. [Click here to view] |
Preparation of suppositories by fusion molding
The preparation consisted in melting the quantity of PEG 6000 of each formulation at 46°C in the stainless steel capsule, then adding the other components under agitation (risk of gelation of the mass) and without incorporation of air bubbles. The prepared suppositories was scraped and stored in glass bottles.
Chemical and pharmaco-technical assay of the prepared suppositories
The prepared suppositories have been evaluated following the USP monographs for appearance, weight variation, content uniformity of dosage form, hardness, disintegration time, and dissolution assay. The Barbital content was determined using a UV–visible spectrophotometer. The hardness was performed with the Erweka AR 400 hardness tester (Erweka Apparatebau-GmbH Germany). The disintegration was performed in a 6.8 pH buffer solution at 37°C (+/−0.5) using the U.S.P. tablet disintegration apparatus (SOTAX DT 3, Heusenstamm, Germany).
Dissolution testing
The suppository was placed in the basket, lowered to the precise level in 1L vials filled with 500 ml phosphate buffer (pH 7.2), and conditioned at 37°C ± 0.5. The basket apparatus was set at 50 rpm. Three millilitre of the dissolution medium was withdrawn with a syringe at defined time intervals (t20, t50, t80, t160, and t235 minutes). The volume withdrawn was replaced by its equivalent in phosphate buffer. The optical density of the filtrate (filters 0.24 μm) was measured at 245 nm with the UV-visible spectrophotometer (Spectrophotometer 6305 UV-VIS 198 at 1000 nm Jenway, Bibby Scientific France SAS) (Onyeji et al., 1999; Özgüney et al., 2007; Ranjita and Kamalinder, 2010).
Modeling dissolution kinetics
For modified release suppositories, the release of the active principle is due to different parameters such as disintegration, diffusion of the active principle through a membrane, swelling, and diffusion through a polymer, erosion of a matrix (Costa and Lobo, 2001; Faisant et al., 2002; Varma et al., 2004). Various kinetics models were used to describe the release kinetics (Faisant et al., 2002; Peppas and Narasimhan, 2014).
The zero-order model (Equation 1) is applied to pharmaceutical forms that do not disintegrate and that release the product over a long period of time. These are of matrix modified-release forms with poorly soluble active ingredients, coated forms and osmotic forms (Moodley et al., 2012). The first-order model (Equation 2) was proposed by Wagner for forms whose release depends on pH (Basak et al., 2008). The Higuchi model (Equation 3) is applicable if diffusion is the only mechanism responsible for the release of the active ingredient (Craig, 2002). The Korsmeyer–Peppas model (Equation 4) is used to classify drug release from polymers as fickian and non-fickian (Güneri et al., 2004). The Hixson–Crowell model (Equation 5) describes the release of systems in which the surface area and diameter of the matrix change over time (Dash et al., 2010).
The so-called Zero Order:
Q0 = K0t (1)
The first-order model:
Q1 = (1 −e−kt) (2)
The Higuchi kinetics model:
QKp = kKPtn (3)
The Korsemyer–Peppas kinetics model:
QH = KH tn (4)
Hixson–Crowell model
QHC={1−(1−KHCt)3} (5)
where Q is the cumulative percent of drug release of Barbital, Q0, QH, QKP, and QHC are the intercepts of the models, k0, K1, KHC, and KKP are the rate of release, n is the diffusional exponent indicating the drug-release mechanism. When the values of n equal to 0.5, the drug release, follow the Fickian diffusion law. When 0.5 < n < 1, the drug release follow a non-Fickian diffusion. When n = 1.0, the drug release is caused by swelling of the polymer (Costa and Lobo, 2001; Zhang et al., 2010).
Statistical analysis
Frequentist approaches study the behaviour of the data, i.e., the probability of repetition of events. Bayesian approaches are based on the measurement of uncertainty.
Frequentist approach
Data of each Formulation were fitted individually to the five above-mentioned models using DD-Solver which is an add-in program in Microsoft Excel. DD-Solver uses the nonlinear least-squares fitting technique, and models parameters were determined based by minimizing the sum of squares errors (Nakata, 2010; Zuo et al., 2014). The initial values of the model were set individually before the iterative optimization. The best model for each formulation is selected based on several criteria such as R-sq Adjusted and AIC. Both Rsq and AIC present a limitation in the model selection and inference process when the number of parameters are different between candidate models (Nakata, 2010). In addition, the DD-solver does not allow for hierarchization of one or all model parameters. Given that, the selected model (best-fitting model) may vary from formulation to another in particular when the number of points in the curve is limited (Nakata, 2010).
Bayesian approach
Data of all formulations were fitted to the five above mentioned models using a hierarchical Bayesian model using the PyMC3 packages of Python (Patil et al., 2010; Salvatier et al., 2016). This approach assumes that the formulations share the same best model and differ only on values of some or all parameters of the model, for each of the five models. Prior parameters of each model were as follows: the variation was assumed zero and model parameters were set to the initial value obtained when the model was fitted to all data.
The trace plot, the posterior distribution of the parameters over each Markov chain Monte Carlo (MCMC) and the convergence of the chains were used to examine the performance of the models (Bates and Campbell, 2001; Cowles and Carlin, 1996). MCMC is a class of algorithms which can efficiently characterize even high dimensional posterior distributions through drawing of randomized samples such that the points are distributed according to the posterior. For each model, chain MCMC of 2000 cycles were considered with a burn-in period of first 200 cycles.
We used two methods for Bayesian model selection such as the widely applicable information criterion (WAIC) and Leave-one-out cross-validation (LOO) (Vehtari et al., 2017; Watanabe and Opper, 2010). The methods evaluate models based on their predictive validity. LOO method examines each left out piece of data, the performance of the model. WAIC uses the entire posterior distribution of models to assess model performance (Gelman et al., 2014; Luo and Al-Harbi, 2017; Vehtari et al., 2015). Widely available information criterion is calculated as Gelman et al. (2014) as:
WAIC = −2lppd + 2pWAICn (6)
The lppd is the log point-wise predictive density and can be approximated as:
lppd = ∑log (Epostp (yi|θ)) (7)
and
pWAICn = ∑varpostlog(p(yi|θ)) (8)
The simpler way to perform model selection is to rank models based on their WAIC or LOO value and to choose the model with the lowest one, However, this simple method do not take in to account the uncertainty of WAIC of each model given the standard error of WAIC. As such, we performed a model selection calculating an average weight for each model relative to the best model (the lowest WAIC or LOO):
wi = exp (−1/ 2dICi)/ ∑j Mexp (−1/2dICj) (9)
where wi is the weight of the model i, which corresponds to its relative probability relative to all tested models.
For the model selection, we have five hierarchical models cited above, in addition we add the corresponding pooled models for each category of the model, which aim to test the hypothesis of the significant effect of the quantities of the two Eudragits on the rate of release. In other words, the selection of hierarchical model corresponds to a significant effect of Eudragits quantities on release rate; inversely the selection of pooled model corresponds to the lack of effect of Eudragits quantities on the kinetic of release.
The effect of Eudragits on the release rate was assessed by investigating the relationship between the parameters of the selected model and the weight of EL-100 or ES-100 in the formulation using the non-linear regression technique in Scipy package.
RESULTS AND DISCUSSION
All suppositories satisfy the requirement of the European pharmacopeia content uniformity, weight variation, hardness, and disintegration time. Although, the uniformity of content varied from 96.1% to 101.5%, and the weight variation from 2.23 to 2.67 g. The hardness of all formulations was superior to 4.8 kg and the disintegration time ranged between 30 and 203 minutes.
In vitro release modeling
In vitro dissolution tests have shown that the prepared suppositories have an sustained-release effect, even if it does not contain Eudragit (formulation No. 13 with PEG 6000 only). The percentage of Barbital dissolved in 4 hours (235 minutes) was more than 90% for four formulations (F3, F5, F12, and F13), more than 80% for formulations F2, F6, F7, and F8 and less than 80% for five formulations (F1, F4, F9, F10, and F11).
Frequentist model selection approach
In vitro release characteristics of sustained-release suppositories were evaluated to determine the best-fitted kinetic model (Table 2). The release rates of all formulations were best described with first-order model, which presented an Rsq (Adjust) > 0.90 and AIC < 16 model (Fig. 1). Based on the Rsq(Adjust) ,the first-order model was the best model for formulations 1, 2, 3, 4, 5, 8, and 13, the Higuchi model is best for formulation 9, the Korsmeyer–Peppas model was best for formulations 6, 10, and 11 and the Hixson–Krowell model was best for both formulations 7 and 12. Based on AIC, the first-order model was best for formulations 1, 2, 3, 4, 5, 8, and 13, Korsmeyer–Peppas is the best model for formulations 9, 10, and 11 and finally the best model for formulations 6 and 7 was Hixson–Krowell (Zhang et al., 2010; Zuo et al., 2014). This showed that the release for the same formulations can have different best models in vitro, which is one of the weaknesses of the Frequentist approach. In fact, the findings from this approach made no clear biopharmaceutical meaning.
Bayesian model selection approach
The first order model presented the lowest value of WAIC and LOO. The standard errors (SE) varied from 3 to 15. The weight of the model was 0.97 and 0.99 based on both WAIC and LOO, respectively. The relative probability (weight) of the selected model was greater than 0.5, indicating that no competing model was possible. The LOO and WAIC estimate the same predictive performance criteria. The selection of the pooled model represented the H0 hypothesis, i.e., K1 is not affected by the quantities of the two Eudragits, while the selection of the hierarchical model represented the alternative hypothesis, i.e., K1 is affected by the quantities of the two Eudragits. According to results, the alternative hypothesis H1 was accepted, the quantities of the two Eudragits have a significant effect on K1. (Tables 3 and 4). The Bayesian estimation of the parameters of the selected model was completed based on the posterior normal distribution of the estimate. The Markov chain has stabilized as indicated by the trace plot (Fig. 2). The posterior distribution of the parameter of the best model (K1) was normal for all formulations. The estimated K1 varied from 0.006 to 0.012 and it SE from 0.0001 to 0.001. The SE of the model was 6.154 based on WAIC and 6.4 based on LOO, which confirms the strength of the results. LOO and WAIC estimated the same predictive performance criteria and were asymptotically equal (Gelman et al., 2014; Vehtari et al., 2016; Vehtari and Ojanen, 2012).
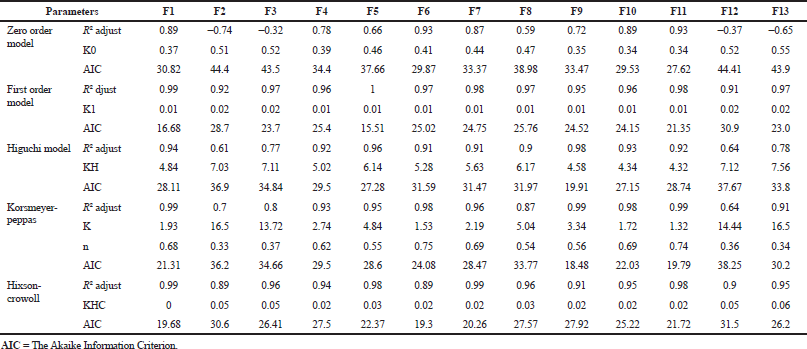 | Table 2. The Rsq (Adjust) and AIC for the release kinetics of Barbital using different mathematical models obtained by DD-Solver. [Click here to view] |
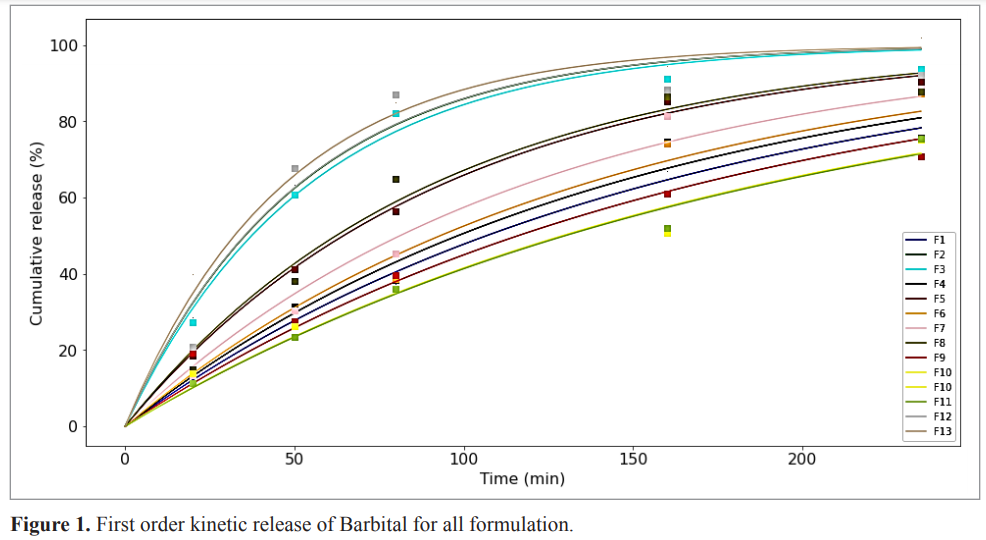 | Figure 1. First order kinetic release of Barbital for all formulation. [Click here to view] |
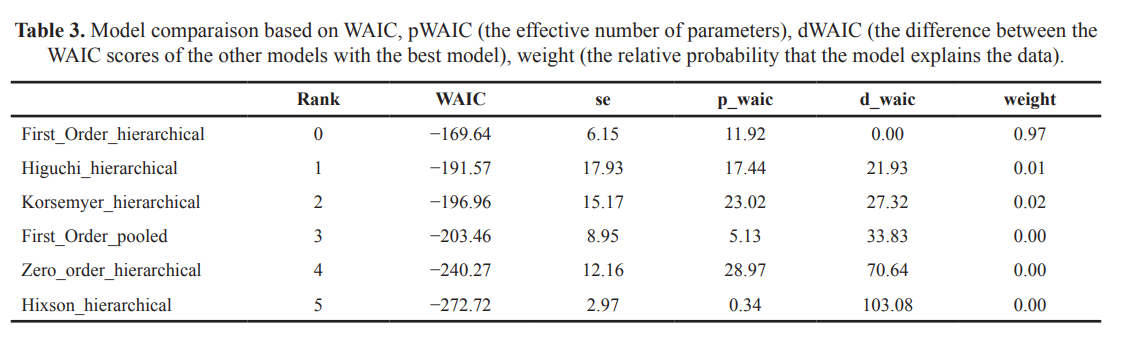 | Table 3. Model comparaison based on WAIC, pWAIC (the effective number of parameters), dWAIC (the difference between the WAIC scores of the other models with the best model), weight (the relative probability that the model explains the data). [Click here to view] |
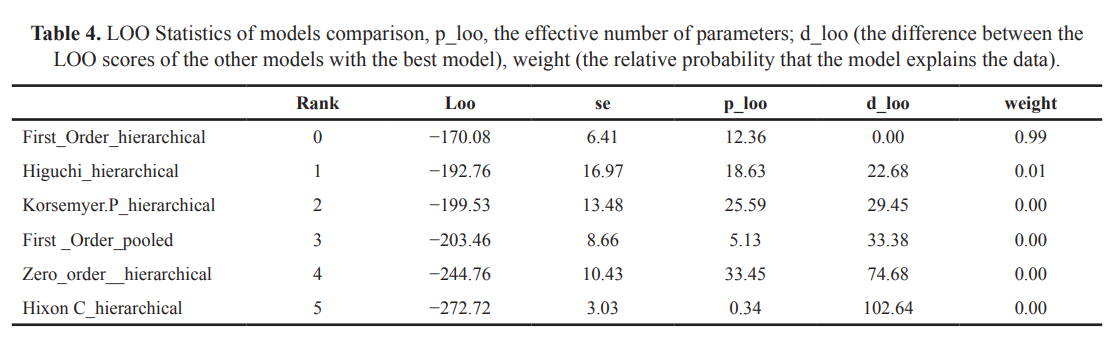 | Table 4. LOO Statistics of models comparison, p_loo, the effective number of parameters; d_loo (the difference between the LOO scores of the other models with the best model), weight (the relative probability that the model explains the data). [Click here to view] |
The hierarchical method gives a single stable model (First-order model) for the same series of formulations whereas the standard method (frequentist approach) gives several models. The K1 of the first-order model estimated by frequentist and Bayesian method were strongly significantly related (Fig. 3). The Bayesian method gave a good estimate of observed data (Fig. 4) and was used for further analysis (VanderPlas, 2014). The relationship between K1 and the quantities of the two Eudragits was quadratic (Equation 10). The release rate (K1) was low for Eudragit L values up to 0.5 g (2.5%) and increases until it reaches its maximum at 2 g (10%) of this Eudragit, on the contrary for Eudragit S, K1 decrease from 0 g to reach it minimum at 1.5 g (7.5%) (Fig. 5).
Y = 0.0031 X2 − 0.0026 X + 0.0069 (Req = 0.8214) (10)
with K = −2b/a = 02*0.0026/0.0031 = 0.41
By this equation which relates the rate of dissolution to the quantity of EL-100, and therefore the mixing of the two Eudragits (total =10%). Drug release from suppository bases generally depends upon the drug solubility in the base and chemical composition of the base. Barbital is a drug in the sodium salt form with a high affinity for hydrophilic bases, i.e., PEG 6000. PEG bases are also known to have a solubility effect, which may partly explain the higher drug release rates of t20 minutes formulations. Both Eudragits create a swellable matrix through which water-soluble active ingredients are released. The mixture advantage became in the difference in solubility of the two polymers in a range of pH =7 to 8, i.e., with EL-100 Intestinal soluble-fluid from (pH 6) and ES-100 is intestinal soluble-fluid from (pH 7) (Di Colo et al., 2002; Hong et al., 2013). The first-order kinetics model as validated by the Bayesian method as the most adequate model to describe and predict the release of active ingredient, this result is due to the dissolved matrix as a function of the pH of the rectal region (Dash et al., 2010). Gibaldi and Feldman were the first to propose first-order kinetic models of liberation in 1967, followed by Wagner in 1969, for this model the rate of liberation depends on concentration (Costa and Lobo, 2001).
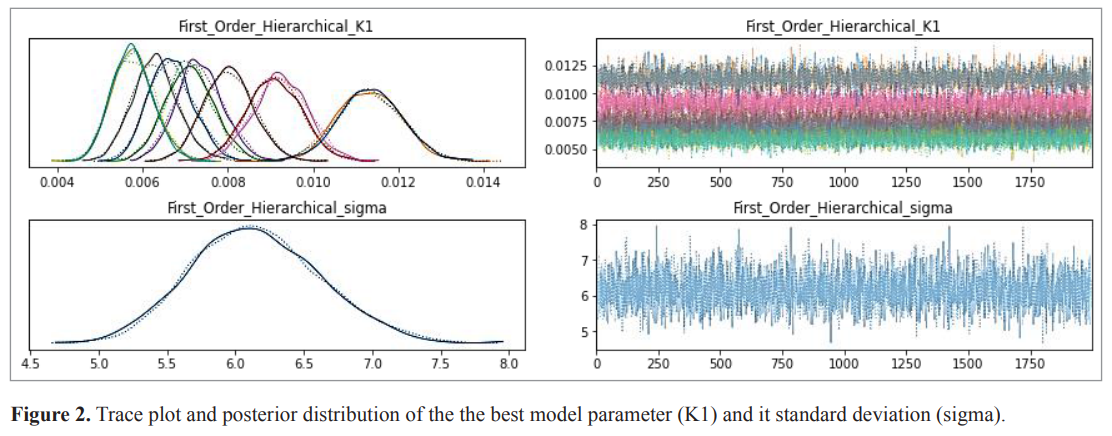 | Figure 2. Trace plot and posterior distribution of the the best model parameter (K1) and it standard deviation (sigma). [Click here to view] |
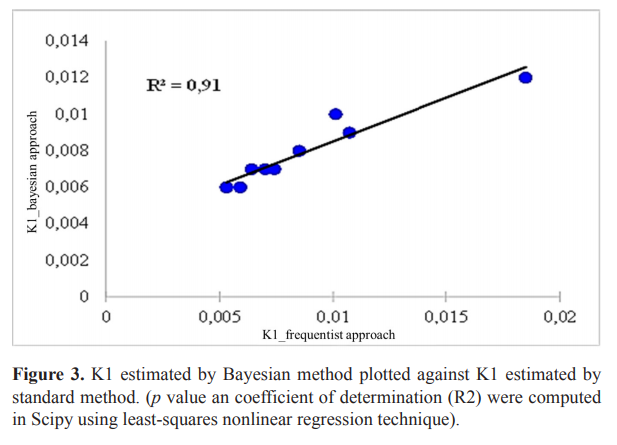 | Figure 3. K1 estimated by Bayesian method plotted against K1 estimated by standard method. (p value an coefficient of determination (R2) were computed in Scipy using least-squares nonlinear regression technique). [Click here to view] |
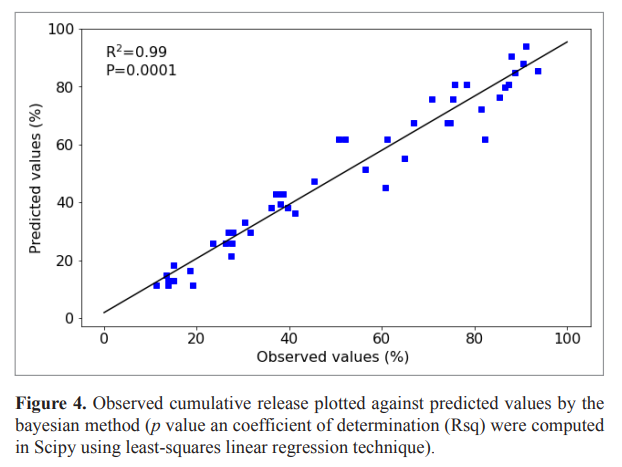 | Figure 4. Observed cumulative release plotted against predicted values by the bayesian method (p value an coefficient of determination (Rsq) were computed in Scipy using least-squares linear regression technique). [Click here to view] |
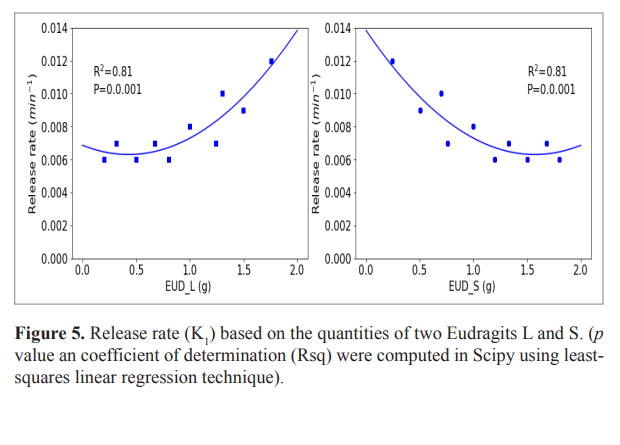 | Figure 5. Release rate (K1) based on the quantities of two Eudragits L and S. (p value an coefficient of determination (Rsq) were computed in Scipy using least-squares linear regression technique). [Click here to view] |
CONCLUSION
In this study, Bayesian approach was applied to drug release modeling and formulation of sustained-release suppositories containing a mixture of EL-100 and ES-100. This approach allowed finding a unique and the most adequate model, which was the first-order model, when the standard frequentist approach gave three best models. At the same time, the Bayesian approach is a tool for predicting the optimal composition for the formulation of a suppository with prolonged effect. In drug development field, this represented an original and new way to master the kinetics modeling of sustained-release products in order to minimize the number of experiments, save time, and save expensive chemicals.
ACKNOWLEDGMENTS
We thank Dr. Lahcen Benomar (University of Quebec in Abitibi-Temiscamingue) for his help with statistical analyses. Special thanks are also extended to Dr. Mohamed Taha Moutaoufik (University of Regina) and Read Elfarjani ( TELUQ University) for their valuable comments and suggestions. We thank the reviewers and the editor for relevant comments that helped to improve the content of this article.
AUTHOR CONTRIBUTIONS
All authors made substantial contributions to conception and design, acquisition of data, or analysis and interpretation of data; took part in drafting the article or revising it critically for important intellectual content; agreed to submit to the current journal; gave final approval of the version to be published; and agree to be accountable for all aspects of the work. All the authors are eligible to be an author as per the international committee of medical journal editors (ICMJE) requirements/guidelines.
FUNDING
There is no funding to report.
CONFLICTS OF INTEREST
The authors report no financial or any other conflicts of interest in this work.
ETHICAL APPROVALS
This study does not involve experiments on animals or human subjects.
PUBLISHER’S NOTE
This journal remains neutral with regard to jurisdictional claims in published
REFERENCES
Andrews RL, Ansari A, Currim . Hierarchical Bayes versus finite mixture conjoint analysis models: A comparison of fit, prediction, and partworth recovery. J Market Res, 2002; 39(1):87–98. CrossRef
Basak SC, Kumar ,Ramalingam M. Design and release characteristics of sustained release tablet containing metformin HCl. Rev Brasil Ciências Farmacêuticas, 2008; 44(3):477–83. CrossRef
Bates BC, Campbell . A Markov chain Monte Carlo scheme for parameter estimation and inference in conceptual rainfall-runoff modeling. Water Resour Res, 2001; 37(4):937–47. CrossRef
Costa P, Lobo . Modeling and comparison of dissolution profiles. Eur J Pharm Sci, 2001; 13(2):123–33. CrossRef
Cowles MK, Carlin BP. Markov chain Monte Carlo convergence diagnostics: a comparative review. J Am Stat Assoc, 1996; 91(434):883–904. CrossRef
Craig DQ. The mechanisms of drug release from solid dispersions in water-soluble polymers. Int J Pharma, 2002; 231(2):131–44. CrossRef
Dash S, Murthy , Nath L, Chowdhury P. Kinetic modeling on drug release from controlled drug delivery systems. Acta Pol Pharm, 2010; 67(3):217–23.
Di Colo G, Falchi S, Zambito Y. In vitro evaluation of a system for pH-controlled peroral delivery of metformin. J Control Release, 2002; 80(1–3):119–28. CrossRef
Faisant N, Siepmann J, Benoit J-P. PLGA-based microparticles: elucidation of mechanisms and a new, simple mathematical model quantifying drug release. Eur J Pharm Sci, 2002; 15(4):355–66. CrossRef
Gelman A, Hwang J, Vehtari A. Understanding predictive information criteria for Bayesian models. Stat Comput, 2014; 24(6):997–1016. CrossRef
Gouda R, Baishya H, Qing Z. Application of mathematical models in drug release kinetics of carbidopa and levodopa ER tablets. J Dev Drugs, 2017; 6(02). CrossRef
Grassi M, Grassi G, Lapasin R, Colombo I. Understanding drug release and absorption mechanisms: a physical and mathematical approach. CRC Press, Boca Raton, FL, 2006. CrossRef
Güneri T, Arici M, Ertan G. Sustained release suppositories of ibuprofen microspheres. FABAD J Pharm Sci, 2004; 29:177–84.
Hong H, Carlin , Shamliyan , Wyman , Ramakrishnan R, Sainfort F, Kane . Comparing Bayesian and frequentist approaches for multiple outcome mixed treatment comparisons. Med Decision Making, 2013; 33(5):702–14. CrossRef
Hua S. Physiological and pharmaceutical considerations for rectal drug formulations. Front Pharmacol, 2019; 10:1196. CrossRef
Joshi M. Role of eudragit in targeted drug delivery. Int J Curr Pharm Res, 2013; 5(2):58–62.
Khan MZI, Prebeg Ž, Kurjaković N. A pH-dependent colon targeted oral drug delivery system using methacrylic acid copolymers: I. Manipulation of drug release using Eudragit® L100-55 and Eudragit® S100 combinations. J Control Release, 1999; 58(2):215–22. CrossRef
Lee SH, Bajracharya R, Min , Han , Park , Han . Strategic approaches for colon targeted drug delivery: an overview of recent advancements. Pharmaceutics, 2020; 12(1):68. CrossRef
Luo Y, Al-Harbi K. Performances of LOO and WAIC as IRT model selection methods. Psychol Test Assess Model, 2017; 59(2):183.
Malekmohammadi S, Hadadzadeh H, Rezakhani S, Amirghofran Z. Design and synthesis of gatekeeper coated dendritic silica/titania mesoporous nanoparticles with sustained and controlled drug release properties for targeted synergetic chemo-sonodynamic therapy. ACS Biomater Sci Eng, 2019; 5(9):4405–15. CrossRef
Millar RB. Comparison of hierarchical Bayesian models for overdispersed count data using DIC and Bayes’ factors. Biometrics, 2009; 65(3):962–9. CrossRef
Misra A. 2014. Applications of polymers in drug delivery. Shrewsbury, United Kingdom: Smithers Rapra.
Moodley K, Pillay V, Choonara YE, Du Toit LC, Ndesendo VM, Kumar P, Cooppan S, Bawa P. Oral drug delivery systems comprising altered geometric configurations for controlled drug delivery. Int J Mol Sci, 2012; 13(1):18–43. CrossRef
Nakata M. A numerical evaluation of highly accurate multiple-precision arithmetic version of semidefinite programming solver: SDPA-GMP,-QD and-DD. IEEE International Symposium on Computer-Aided Control System Design, IEEE, Denver, CO, 2010. CrossRef
Natanegara F, Neuenschwander B, Seaman Jr JW, Kinnersley N, Heilmann CR, Ohlssen D, Rochester G. The current state of Bayesian methods in medical product development: survey results and recommendations from the DIA Bayesian Scientific Working Group. Pharm Stat, 2014; 13(1):3–12. CrossRef
Nikam VK, Kotade K, Gaware V, Dolas R, Dhamak K, Somwanshi S, Khadse A, Kashid V. Eudragit a versatile polymer: a review. Pharmacology, 2011; 1(5):152–64.
Onyeji CO, Adebayo AS, Babalola CP. Effects of absorption enhancers in chloroquine suppository formulations: I: In vitro release characteristics. Eur J Pharm Sci, 1999; 9(2):131–6. CrossRef
Özgüney I, Özcan Ä°, Ertan G, Güneri T. The preparation and evaluation of sustained release suppositories containing ketoprofen and Eudragit RL 100 by using factorial design. Pharm Dev Technol, 2007; 12(1):97–107. CrossRef
Paarakh MP, Jose PA, Setty C, Christoper G. Release kinetics–concepts and applications. Int J Pharm Res Technol, 2018; 8(1):12–20.
Patil A, Huard D, Fonnesbeck CJ. PyMC: Bayesian stochastic modelling in Python. J Stat Softw, 2010; 35(4):1. CrossRef
Peppas NA, Narasimhan B. Mathematical models in drug delivery: how modeling has shaped the way we design new drug delivery systems. J Control Release, 2014; 190:75–81. CrossRef
Piray P, Dezfouli A, Heskes T, Frank MJ, Daw ND. Hierarchical Bayesian inference for concurrent model fitting and comparison for group studies. PLoS Comput Biol, 2019; 15(6):e1007043. CrossRef
Price K, LaVange L. Bayesian methods in medical product development and regulatory reviews. Pharm Stat, 2014; 13(1):1–2 CrossRef
Ranjita S, Kamalinder S. In-vitro release of paracetamol from suppocire suppositories: role of additives. In vitro, 2010; 8(1):57–71.
Salvatier J, Wiecki TV, Fonnesbeck C. Probabilistic programming in Python using PyMC3. PeerJ Comput Sci, 2016; 2:e55. CrossRef
Surti N, Mahajan A, Misra A. Polymers in rectal drug delivery. Applications of polymers in drug delivery. Elsevier, Amsterdam, Netherlands, 2020, pp 263–80. CrossRef
Thakral S, Thakral NK, Majumdar DK. Eudragit®: a technology evaluation. Expert Opin Drug Deliv, 2013; 10(1):131–49. CrossRef
VanderPlas J. 2014. Frequentism and bayesianism: a python-driven primer. arXiv. [ONLINE] Available at: https://arxiv.org/abs/1411.5018. [Accessed 20 January 2021]. CrossRef
Varma MV, Kaushal AM, Garg A, Garg S. Factors affecting mechanism and kinetics of drug release from matrix-based oral controlled drug delivery systems. Am J Drug Deliv, 2004; 2(1):43–57. CrossRef
Vehtari A, Gelman A, Gabry J. 2015 . Efficient implementation of leave-one-out cross-validation and WAIC for evaluating fitted Bayesian models. ArXiv. [ONLINE] Available at: https://arxiv.org/. [Accessed 20 January 2021].
Vehtari A, Gelman A, Gabry J. Practical Bayesian model evaluation using leave-one-out cross-validation and WAIC. Stat Comput, 2017; 27(5):1413–32. CrossRef
Vehtari A, Mononen T, Tolvanen V, Sivula T, Winther O. Bayesian leave-one-out cross-validation approximations for Gaussian latent variable models. J Mach Learn Res, 2016; 17(1):3581–618.
Vehtari A, Ojanen J. A survey of Bayesian predictive methods for model assessment, selection and comparison. Stat Surv, 2012; 6:142–228. CrossRef
Victor O, Francis O. Evaluation of the kinetics and mechanism of piroxicam release from lipophilic and hydrophilic suppository bases. Int J Chem Tech Res, 2017l 10:189–98.
Watanabe S, Opper M. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J Mach Learn Res, 2010; 11(12):3571–94.
Wiecki TV, Sofer I, Frank MJ. HDDM: hierarchical Bayesian estimation of the drift-diffusion model in python. Front Neuroinform, 2013; 7:14. CrossRef
Zhang Y, Huo M, Zhou J, Zou A, Li W, Yao C, Xie S. DDSolver: an add-in program for modeling and comparison of drug dissolution profiles. AAPS J, 2010; 12(3):263–71. CrossRef
Zuo J, Gao Y, Bou-Chacra N, Löbenberg R. Evaluation of the DDSolver software applications. Biomed Res Int, 2014; 2014:204925. CrossRef