INTRODUCTION
Rosemary (Rosmarinus officinalis L.), as a perennial herb belonging to Lamiaceae family, is utilized in cosmetics, in traditional medicine, and as a food preservative and flavoring agent (Ramírez et al., 2006). This plant has high antioxidant activity, antimicrobial, and antimutagenic characteristics, and is also known as a chemopreventive agent (Ibañez et al., 2003; Oluwatuyi et al., 2004). Rosemary has been found to have abundant essential oil in the flower and in the leaves. While oil extraction can be done from both locations, the leaves containing essential oil glands have the most high-quality essential oil (Carvalho et al., 2005).
Because of its utilization in several applications, such as food preservatives, cosmetics, and pharmaceutical medicines, extracting essential oils from aromatic plants is a highly essential research topic. A variety of oil extraction methods are applied for medicinal plants, for instance, rosemary plant, including steam distillation, percolation, hydrodistillation (HD), supercritical fluid extraction, and ultrasound and microwave-assisted extractions (Belhachat et al., 2018; Presti et al., 2005).
Extracting essential oils by microwave-assisted hydrodistillation (MHD) is more utilized in both laboratories and industries because of many features, such as rapid energy transfer and efficient heating, in addition to the environmentally eco-friendly isolation system (Filly et al., 2014). The MHD in comparison with other conventional methods of extraction, such as HD, shows high performance in terms of improvement of quality, as well as quantity of the isolated oils, reduction for the extraction time, and reduction in both cost and energy consumption, as well as the minimization of the carbon dioxide quantity emitted into the atmosphere (Elyemni et al., 2019; Karakaya et al., 2014; Moradi et al., 2018).
Generally, MHD extraction efficiency can be affected by several variables, alone or in combination, which includes extracting time, water-to-plant ratio, the microwave power supply, and drying time (Benmoussa et al., 2018; Mathialagan et al., 2014; Turk et al., 2018). Hence, it is necessary to optimize these parameters to obtain a higher yield.
Traditionally, the optimization studies are conducted using a classical optimization method called one-variable-ata-time, where one variable changes at a time but others remain unchanged (Kannan et al., 2004). In such a method, the main drawback is that the excluded interactive influences found between variables and experimental work required are increased, leading to increased time usage, cost, and use of reagents and materials (Bezerra et al., 2008).
Response surface methodology (RSM), as a solution to the above-mentioned issue, is highly recommended because of its ability to optimize experimental conditions for a multivariable system, while decreasing the number of needed experimental trials for evaluating several parameters and their interactions. RSM is useful in different methods, including central composite design (CCD) and Box–Behnken design, in addition to a three-level full factorial design (BaÅŸ and Boyacı, 2007; Montgomery, 2017). Recently, RSM has been successfully employed in chemistry, biology, food, agriculture, engineering, and other research fields (Bashir et al., 2010; Hasani et al., 2019; Sharma et al., 2018; Sodeifian et al., 2018).
In our work, we aim to employ RSM in terms of exploration as well as optimization of several variables, such as the extraction time, water-to-plant ratios, microwave power, and finally the drying period for extraction of rosemary essential oil by MHD.
MATERIALS AND METHODS
Plant material
Freshly harvested rosemary aerial parts were realized at the stage of flowering in May 2018, located in Fez region. The dried plant was attained when left in the shade at 25°C for 7 or 14 days.
Microwave-assisted hydrodistillation
The MHD was accomplished with the assistance of a microwave oven as a power supply, with specifications of MWD 119 WH, whirlpool, China, 20 L, 2.45 GHz, that had a direct connection with a Clevenger appliance as well as a cooling system for continuous condensation of the distillate. The microwave oven has a power consumption of 1,100 Watts and an output power of 700 Watts, with a power source of 230 v–50 Hz with cavity dimensions of 216 × 302 × 277 mm.
In the MHD procedure, 100 g of fresh or dried rosemary samples was mixed with various volumes of water (200, 400, and 600 ml) in a flask (2 l) and heated inside the microwave oven cavity at various powers (200–600 W) and various extraction times (20–90 minutes). The vapor mixture of water and essential oil was condensed continuously within a cooling system at the exterior of the microwave cavity and recovery was attained in a Clevenger receiving. The excess condensed water was refluxed into the flask of extraction for providing unvarying environments of humidity for the extraction process (Elyemni et al., 2019). Subsequently, the essential oils collected were charged with anhydrous sodium sulfate to be dehydrated, weighed, and finally stored at 4°C in a vial in the dark.
Experimental design of RSM and statistical analysis
To define the optimum conditions, a three-level-four-factor CCD, followed by RSM, was utilized, affording the highest yield of the extracted essential oil derived from rosemary and aided by the MHD. The independent variables studied were extracting time, microwave power supply, water-to-plant ratio, and drying period, whereas the essential oil extraction yield was the response variable, which is calculated by using:
The central point and range of the four variables had been chosen depending on the preliminary experiments’ outcomes. In each parameter, three levels were examined and have different codes as follows: –1 for lower level, +1 for higher level, and 0 for a central coded value as shown in Table 1.
According to CCD, 30 experimental runs were proposed that comprise 16 factorial runs and 8 axial runs in addition to 6 replicate runs at the center. The center point replicates can provide a pure error estimate, and experiments were conducted randomly to prevent systematic error. The experimental design in addition to statistical analysis was achieved by Design Expert 11 Trial. The response employed for establishing an empirical model that linked response to four input variables by means of a second-degree polynomial is displayed as:
where Y represents the response function, β0 is the intercept term, Xi and Xj are coded independent parameters, βi are linear coefficients, βii are quadratic coefficients, βij are interaction coefficients, and ε is the experimental error (Benmoussa et al., 2018; Mathialagan et al., 2014).
Statistical examination of the model was realized using the analysis of variance (ANOVA) analysis as well as the F-test for exploring the ideal relationship between input factors and extraction yield. Each term’s significance in the equation of the model was evaluated statistically when the corresponding p-values (significance confirmed if p ≤ 0.05) were calculated (Ara and Raofie, 2016; Rai et al., 2016). For evaluating the model reliability, coefficient of determination (R2), adjusted R2, predicted R2, lack of fit, and adequate precision were used. The response surfaces and contours plots were created for determining the individual test variables or interactive effects on essential oil yield and to deduce the optimum conditions.
 | Table 1. Experimental variables and their levels. [Click here to view] |
RESULTS AND DISCUSSION
The experimental design together with the experimental extraction values in the presence of various combined extraction settings is presented in Table 2.
Response ranges from 0.034% to 1.331% according to the parameters of the experiments. The maximum yield achieved at MHD is as follows: time of 55 minutes, a microwave power of 600 W, water-to-plant material ratio of 4 ml/g, and drying time of 7 days (run 18).
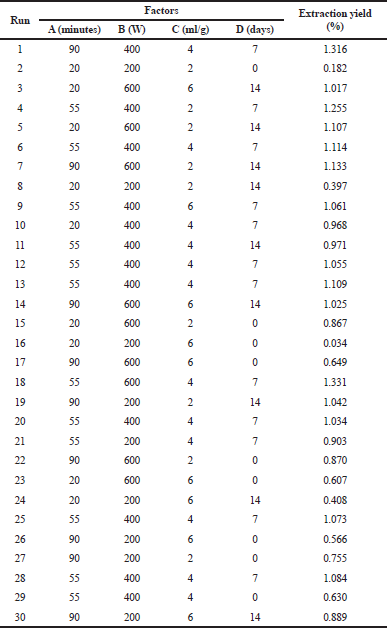 | Table 2. Experimental design matrix and the extraction yield evaluated at various experimental settings. [Click here to view] |
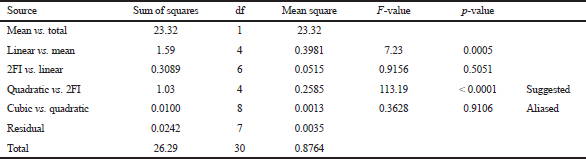 | Table 3. Sequential model sum of squares for MHD of rosemary. [Click here to view] |
Model fitting and ANOVA
The four most widely employed models of linear, two-factor interaction (2FI), quadratic, and cubic models are assessed in accordance with the scores generated by the sequential sum of squares model, and many statistics to evaluate their adequacy are summarized in Table 3 and 4. Compared to other models, the optimal model identified is the quadratic model with the largest F-value of 91.81 and the smallest value of p < 0.0001 (Table 5). Besides, the nonsignificant value of the lack of fit (p-value of 0.1130 > 0.05) for the quadratic model revealed the validity of this model, with better credibility and accuracy (Qi et al., 2014).
The equation for the second-order polynomial regression is presented as follows, regarding the coded factors obtained from the software:
The coefficients’ sign and magnitude allow the interpretation of the variable effects on the response. The quadratic model showed a positive impact on the yield extracted for the linear variables A, B, and D, the interactions of the variables AD, BD, and CD, and the variable quadratic C2, while the variables C, AB, AC, and BC and the quadratic variables A2, B2, and C2 exhibited adverse consequences.
As Table 3 shows, the ANOVA of the quadratic polynomial model selected for MHD of rosemary revealed R2 determination coefficient as of 0.9885, signifying the ability of the model to explain 98.85% of the data variation, while it has no explanation for only 1.15% of the total variations.
The adjusted R2 (0.9777) value was precisely close to its corresponding R2, which suggests a strong correlation of the observed and anticipated data. The difference between the adjusted and predicted R2 should therefore be less than 0.2 to be in judicious matching (Owolabi et al., 2018; Rai et al., 2016). This requirement is satisfied with a predicted R2 value of 0.9564.
The data dispersion is described by the coefficient of variation (CV), where reproducibility with better values was achieved at lower values of CV% (< 10%) (Zhang et al., 2014). For the suggested models, such value is 4.35% denoting high precision and reliability (Table 5). Finally, the value of “adequate precision” of 35.2024 is greater than 4, suggesting an appropriate signal-to-noise ratio (Hu et al., 2018).
 | Table 4. Summary of model statistics for MHD of rosemary. [Click here to view] |
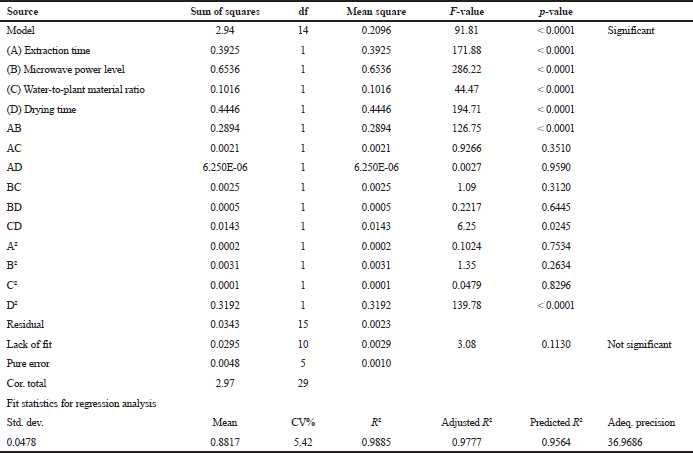 | Table 5. Statistical analysis of variance of the quadratic model generated from CCD for rosemary essential oil extraction yields. [Click here to view] |
The p- and F-values were utilized as an evaluating tool for each coefficient significance of the quadratic model (Table 5), where the smaller the p-value and the higher the F-value, the more important the respective coefficient. In the current work, the significant classification of the factors is B > D > A > D2 > AB > C > CD, while the other coefficients do not affect the extraction yield significantly (p > 0.05). Hence, after ignoring the insignificant terms, the final anticipated polynomial second-order equation attained is given by:
Adequacy of the second-order polynomial models
Three diagnostic plots can confirm the fitted model adequacy, including predicted versus actual plots (Fig. 1a), the normal probability plot against the residual values (Fig. 1b), and the residuals plot against the run number (Fig. 1c).
Figure 1a shows that the values based on the experimental work in comparison with the expected ones were close to being a straight line, offering a well-matched pattern for the determined as well as anticipated values. Such a result supported the least square fit adequacy.
A normal probability plot was generated to check the normality of the internally studentized residual. The proximity of point distributions along the straight lines shows that the residuals for essential oil responses were typically distributed and that the fitted model provided a reasonable estimate to rosemary essential oil’s experimental yields.
The last plot of residuals for rosemary essential oil’s yield against the experimental run order was designed for investigating the practical response and its satisfactory fit (Benmoussa et al., 2018). The diagnostic plot demonstrates that within certain limits (±3) all the data points were distributed unsystematically.
Response surfaces and contour plots analysis
For visualizing the independent variables’ effect in addition to their collaborative interactions on the rosemary extraction yield, three-dimensional response surface and two-dimensional contour plots were built. Two parameters were kept at their central level values coding at a zero, and two different parameters were used for realizing the individual and interactive effect of their response. Response surface plot of extraction yield as a function of extraction time and microwave power (Fig. 2) indicates that the yield of essential oil was positively influenced by the microwave power. Furthermore, at a definite microwave power, the yield of extraction increases with increasing extraction time.
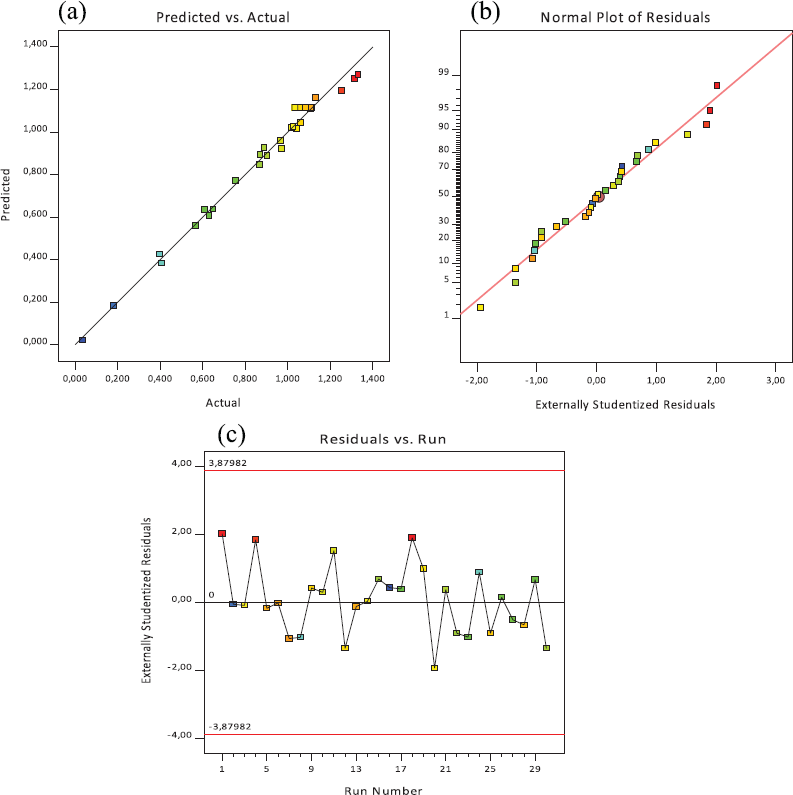 | Figure 1. Diagnostic plots of model adequacy. Predicted versus actual plots (a), normal probability plots of residuals (b), and the residuals versus the run number (c). [Click here to view] |
The improved extraction yield based on increased time of extraction is attributed to the microwave adsorption energy in addition to the interfacial area between the plant matrixes and solvent, which enhances the essential oil dissolution process into the water (Mollaei et al., 2019).
The power of microwaves serves as a driving force to wreck the plant cell membrane structure, which causes the diffusion and the dissolution of the oil in the solvent. Microwave power also has a direct influence on temperature, in which a higher microwave power increases the temperature of the distillation due to the increase in dielectric heating phenomena. Consequently, increased power will usually increase yield and speed up the extraction time (Benmoussa et al., 2018; Chen et al., 2016). The yielded findings are well-matched with those of Mathialagan et al. (2014), who found the equivalent consequence of the microwave irradiation power as well as time on the extracted essential oil yield from the leaves of lemongrass (Cymbopogon citratus) when MHD was employed. Likewise, an extracted essential oil based on Ferulago angulata fruit was realized by microwave-aided hydrodistillation and achieved an equal result described by Mollaei et al. (2019).
Figure 3 shows the influence of the plant-material-to-solvent ratio and drying period on the extraction rosemary essential oil yield at a fixed microwave power of 400 W and fixed extraction time of 40 minutes. The extracted yield decreases slightly with the increase in the plant-material-to-solvent ratio at a constant drying period. This decline was also reached by Abdelhadi et al. (2015) and Mollaei et al. (2019) because of the hydrolyzed volatile ingredients in the presence of high water content. Also, at fixed plant-material-to-solvent ratio and drying period affected the essential oil yield in a quadratic manner. So, low plant-material-to-solvent ratio and moderate drying period were more suitable for the essential oil yield.
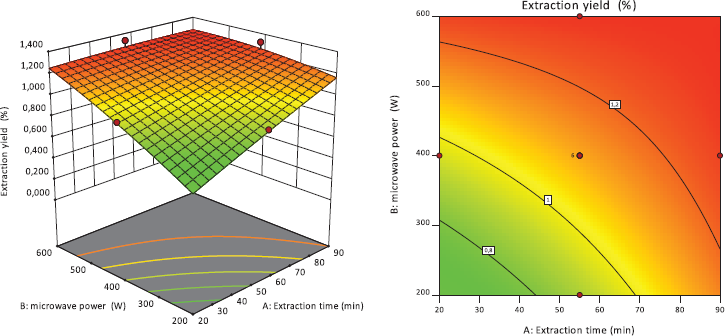 | Figure 2. 3D graphic surface and contour plot for the influence of microwave power level and extraction time on the extraction yield. [Click here to view] |
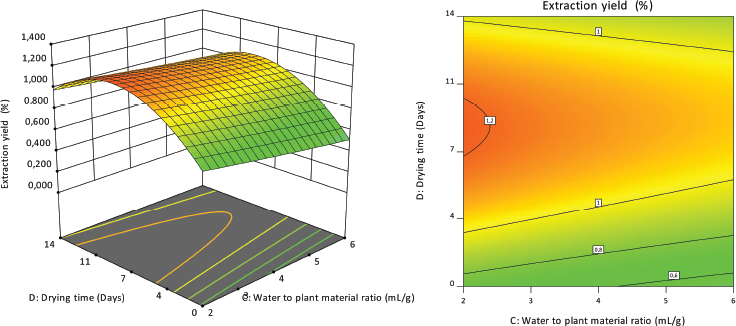 | Figure 3. 3D graphic surface as well as contour plot showing microwave power level and extraction time effects on the extraction yield. [Click here to view] |
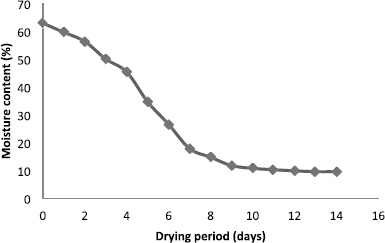 | Figure 4. Evolution of the moisture content of R. officinalis leaves during the drying period. [Click here to view] |
To better explain the effect of drying period on the rosemary essential oil yield, Figure 4 shows the evolution of moisture content according to the drying time.
Regarding the first days, the essential oils rise is proportional to the reduced humidity content, with maximum oil yields between 7 and 9 drying days. Beyond this period, the moisture content tends to stabilize while the yield decreases gradually.
Such results are in accordance with those yielded with other aromatic plants, such as Mentha spicata (Díaz-Maroto et al., 2003), Origanum vulgare (Novák et al., 2011), and Warionia saharae (Essaqui et al., 2016). The rise in the essential oils’ yield using rosemary leaves can be described by a crucial physiological activity and enzymatic reactions during the first days of drying. In fact, the plant after harvest increases its biosynthetic activity of terpenes and derivatives as defense strategies against water stress. When the drying period exceeded 9 days, the essential oils’ yield was decreased because of the decline or discontinuation of biosynthesis activities when the death of cells was realized after extreme dehydration. Consequently, essential oils losses by evaporation are no longer compensated.
Optimization of extraction conditions of R. officinalis essential oil
According to RSM findings, the optimum settings of MHD for maximum yield of rosemary essential oil are a microwave power of 600 W, a time of 20 minutes, a plant-matter-to-water ratio of 2 ml/g, and a drying time of 7 days. At this optimal setting, the rosemary oil yield anticipated was 1.326%. The optimized conditions have been verified experimentally and the extracted oil was identified by gas chromatography-mass spectrometry in a previous work (Elyemni et al., 2019).
CONCLUSION
In the current research, an RSM-based CCD was successfully employed for evaluating the influences of four independent variables, including extraction time, plant-material-to-solvent ratio, and microwave power as well as drying period on the rosemary essential oil yield, and to envisage the ideal operating settings. The experimental findings revealed that microwave power and extraction time were the most substantial parameters influencing the rosemary essential oil extraction yield. The quadratic model established for the extraction yield exhibited a well-matched pattern between the experimental data and model predictions (R2 = 0.9885). The best conditions anticipated by the model for the designated extraction variables are as follows: power microwave (600 W), extraction time (20 minutes), water-to-plant material ratio (2 ml/g), and a drying period (7 days) with a yield of 1.326%.
CONFLICT OF INTEREST
The authors declared that they do not have any conflicts of interest.
FUNDING
None.
REFERENCES
Abdelhadi M, Meullemiestre A, Gelicus A, Hassani A, Rezzoug S. Intensification of Hypericum perforatum L. oil isolation by solvent-free microwave extraction. Chem Eng Res Des, 2015; 93:621–31. CrossRef
Ara KM, Raofie F. Application of response surface methodology for the optimization of supercritical fluid extraction of essential oil from pomegranate (Punica granatum L.) peel. J Food Sci Technol, 2016; 53:3113–21. CrossRef
BaÅŸ D, Boyacı Ä°H. Modeling and optimization I: usability of response surface methodology. J Food Eng, 2007; 78:836–45. CrossRef
Bashir MJK, Aziz HA, Yusoff MS, Adlan MohdN. Application of response surface methodology (RSM) for optimization of ammoniacal nitrogen removal from semi-aerobic landfill leachate using ion exchange resin. Desalination, 2010; 254:154–61. CrossRef
Belhachat D, Mekimene L, Belhachat M, Ferradji A, Aid F. Application of response surface methodology to optimize the extraction of essential oil from ripe berries of Pistacia lentiscus using ultrasonic pretreatment. J Appl Res Med Aromat Plants, 2018; 9:132–40. CrossRef
Benmoussa H, Elfalleh W, He S, Romdhane M, Benhamou A, Chawech R. Microwave hydrodiffusion and gravity for rapid extraction of essential oil from Tunisian cumin (Cuminum cyminum L.) seeds: optimization by response surface methodology. Ind Crops Prod, 2018; 124:633–42. CrossRef
Bezerra MA, Santelli RE, Oliveira EP, Villar LS, Escaleira LA. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta, 2008; 76:965–77. CrossRef
Carvalho RN, Moura LS, Rosa PTV, Meireles MAA. Supercritical fluid extraction from rosemary (Rosmarinus officinalis): kinetic data, extract’s global yield, composition, and antioxidant activity. J Supercrit Fluids, 2005; 35:197–204. CrossRef
Chen F, Du X, Zu Y, Yang L, Wang F. Microwave-assisted method for distillation and dual extraction in obtaining essential oil, proanthocyanidins and polysaccharides by one-pot process from Cinnamomi Cortex. Sep Purif Technol, 2016; 164:1–11. CrossRef
Díaz-Maroto MC, Pérez-Coello MS, González Viñas MA, Cabezudo MD. Influence of drying on the flavor quality of spearmint (Mentha spicata L.). J Agric Food Chem, 2003; 51:1265–9. CrossRef
Elyemni M, Louaste B, Nechad I, Elkamli T, Bouia A, Taleb M, Chaouch M, Eloutassi N. Extraction of essential oils of Rosmarinus officinalis L. by two different methods: hydrodistillation and microwave assisted hydrodistillation. Sci World J, 2019, Article ID 3659432. CrossRef
Essaqui A, Khoudali S, seddiki SE. Drying Effect on yield and chemical composition of essential oils of Warionia saharae from Morocco. J Essent Oil Bearing Plants, 2016; 19:1031–6. CrossRef
Filly A, Fernandez X, Minuti M, Visinoni F, Cravotto G, Chemat F. Solvent-free microwave extraction of essential oil from aromatic herbs: from laboratory to pilot and industrial scale. Food Chem, 2014; 150:193–8. CrossRef
Hasani M, Chudyk J, Murray K, Lim L-T, Lubitz D, Warriner K. Inactivation of salmonella, Listeria monocytogenes, Aspergillus and Penicillium on lemons using advanced oxidation process optimized through response surface methodology. Innov Food Sci Emerg Technol, 2019; 54:182–91. CrossRef
Hu B, Zhou K, Liu Y, Liu A, Zhang Q, Han G, Liu S, Yang Y, Zhu Y, Zhu D. Optimization of microwave-assisted extraction of oil from tiger nut (Cyperus esculentus L.) and its quality evaluation. Ind Crops Prod, 2018; 115:290–7. CrossRef
Ibañez E, Kubátová A, Señoráns FJ, Cavero S, Reglero G, Hawthorne SB. Subcritical water extraction of antioxidant compounds from rosemary plants. J Agric Food Chem, 2003; 51:375–82. CrossRef
Kannan N, Rajakumar A, Rengasamy G. Optimisation of process parameters for adsorption of metal ions on straw carbon by using response surface methodology. Environ Technol, 2004; 25:513–22. CrossRef
Karakaya S, El SN, Karagozlu N, Sahin S, Sumnu G, Bayramoglu B. Microwave-assisted hydrodistillation of essential oil from rosemary. J Food Sci Technol, 2014; 51:1056–65. CrossRef
Mathialagan R, Nour AH, Ziad AS, Azhari HN, ThanaRaj S. Optimization of microwave assisted hydrodistillation of lemongrass (Cymbopogon citratus) using response surface methodology. Int J Res Eng Technol, 2014; 3:5–14. CrossRef
Mollaei S, Sedighi F, Habibi B, Hazrati S, Asgharian P. Extraction of essential oils of Ferulago angulata with microwave-assisted hydrodistillation. Ind Crops Prod, 2019; 137:43–51. CrossRef
Montgomery DC. Design and analysis of experiments. John Wiley & Sons, Hoboken, NJ, 2017.
Moradi S, Fazlali A, Hamedi H. Microwave-assisted hydro-distillation of essential oil from rosemary: comparison with traditional distillation. Avicenna J Med Biotechnol, 2018; 10:22–8.
Novák I, Sipos L, Kókai Z, Szabó K, Pluhár Z, Sárosi S. Effect of the drying method on the composition of Origanum vulgare L. subsp. hirtum essential oil analysed by GC-MS and sensory profile method. Acta Aliment, 2011; 40:130–8. CrossRef
Oluwatuyi M, Kaatz GW, Gibbons S. Antibacterial and resistance modifying activity of Rosmarinus officinalis. Phytochemistry, 2004; 65:3249–54. CrossRef
Owolabi RU, Usman MA, Kehinde AJ. Modelling and optimization of process variables for the solution polymerization of styrene using response surface methodology. J King Saud Univ Eng Sci, 2018; 30:22–30. CrossRef
Presti ML, Ragusa S, Trozzi A, Dugo P, Visinoni F, Fazio A, Dugo G, Mondello L. A comparison between different techniques for the isolation of rosemary essential oil. J Sep Sci, 2005; 28:273–80. CrossRef
Qi X-L, Li T-T, Wei Z-F, Guo N, Luo M, Wang W, Zu Y-G, Fu Y-J, Peng X. Solvent-free microwave extraction of essential oil from pigeon pea leaves [Cajanus cajan (L.) Millsp.] and evaluation of its antimicrobial activity. Ind Crops Prod, 2014; 58:322–8. CrossRef
Rai A, Mohanty B, Bhargava R. Supercritical extraction of sunflower oil: a central composite design for extraction variables. Food Chem, 2016; 192:647–59. CrossRef
Ramírez P, García-Risco MR, Santoyo S, Señoráns FJ, Ibáñez E, Reglero G. Isolation of functional ingredients from rosemary by preparative-supercritical fluid chromatography (Prep-SFC). J Pharm Biomed Anal, 2006; 41:1606–13. CrossRef
Sharma D, Yadav KD, Kumar S. Biotransformation of flower waste composting: optimization of waste combinations using response surface methodology. Bioresour Technol, 2018; 270:198–207. CrossRef
Sodeifian G, Ardestani NS, Sajadian SA, Moghadamian K. Properties of Portulaca oleracea seed oil via supercritical fluid extraction: Experimental and optimization. J Supercrit Fluids, 2018; 135:34–44. CrossRef
Turk M, Mathe C, Fabiano-Tixier A-S, Carnaroglio D, Chemat F. Parameter optimization in microwave-assisted distillation of frankincense essential oil. C R Chim, 2018; 21:622–7. CrossRef
Zhang Y, Cao C, Peng M, Xu X, Zhang P, Yu Q, Sun T. Diversity of nitrogen-fixing, ammonia-oxidizing, and denitrifying bacteria in biological soil crusts of a revegetation area in Horqin Sandy Land, Northeast China. Ecol Eng, 2014; 71:71–9. CrossRef